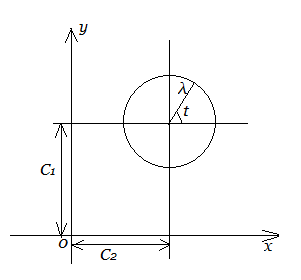
请再次正常理解问题这不是正常不正常的情况下理解别人的问题,只有墙的长度等于60/pai的时候才能围成半圆。
[评论]10年寒窗不如一纸国籍?外籍华人免试入清华北大
- 主题发起人 xchn818
- 发布时间 2018-01-29
Similar threads
2024-09-29有新回复
全楼:0.00
sunny98
- 0.01 超赞 赏
- Saint.Saens ,#416
- 2024-09-02
- 聊天・灌水・娱乐・新闻・时事
2024-09-03有新赞
全楼:0.01
Saint.Saens
- 0.09 超赞 赏
- bfbs ,#210
- 2023-10-26
- 聊天・灌水・娱乐・新闻・时事
2023-10-26有新回复
全楼:0.14
bfbs
2024-10-05有新回复
全楼:0.04
john_smith7777