酷,这个留作以后学习
==================
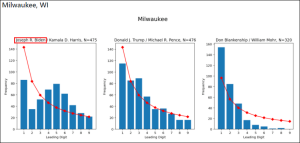
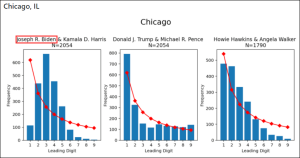
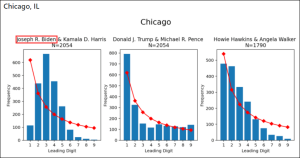
拜登选票作弊无法通过 班福德律(#Benford Law)测验,其他所有候选人都通过。
现在,通过班福德律,可以发现拜登究竟在多少州进行了选票欺诈。
很不幸,估计所有州都做了弊。这里贴的图是密歇根,芝加哥,宾州阿里格内郡...
作弊实锤了,又被逮着了.
班福德律(#Benford Law)测验: 这是根据 一个城市中 所有的 electoral precincts 中, 每位候选人的得票数目来测定的。 可以测出有无作弊.
1的频率最高,接近30.1%
对,有一个北大群专门讨论这个问题,我找来分享
说明数据源被人工干预。
不是只有道理,北大群里讨论就凭这可以提交司法的非常关键的证据
自然发生的“人的行为”数据出现频率是有规律的,而加入人的主观意志干预后发生的数据,概率就特么变了,真是神知道一切啊。[呲牙]
Benford定律产生的原因是因为累加数据的十进位造成的,适用于所有1+1+1..这样一个个产生的数据。我可以解释一下:比方说密西根400个投票站,在投第一票的时候,所有的投票站都是1,这时候统计数据就是1的比例是100%。投第2票的时候,有的投票站产生了2,但是有的投票站产生了川普和拜登各是1,这时候1的占比也很大,2次之。如此下去,有些投票站投的快,会先到达10,这时候如果统计的票数,也是1最多。之后还会首先出现100、111,或者1111,总之累加的数据,1是先出现的,其次是2。按照Benford定律,1的占比概率是30%、2是17%,依次减少。
篡改数据的时候,作弊者不知道本福特定律,所以1和2用的太少了。看密西根的图,他们用了很多的5。
投票特别适合本福特定律,任意时段进行区间统计,都应该符合本福特定律。统计后清零然后继续统计,还是从1开始
==================
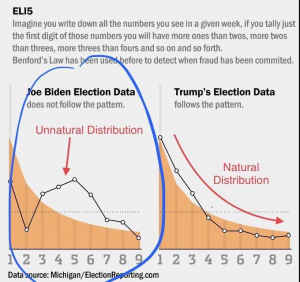
拜登选票作弊无法通过 班福德律(#Benford Law)测验,其他所有候选人都通过。
现在,通过班福德律,可以发现拜登究竟在多少州进行了选票欺诈。
很不幸,估计所有州都做了弊。这里贴的图是密歇根,芝加哥,宾州阿里格内郡...
作弊实锤了,又被逮着了.
班福德律(#Benford Law)测验: 这是根据 一个城市中 所有的 electoral precincts 中, 每位候选人的得票数目来测定的。 可以测出有无作弊.
1的频率最高,接近30.1%
对,有一个北大群专门讨论这个问题,我找来分享
说明数据源被人工干预。
不是只有道理,北大群里讨论就凭这可以提交司法的非常关键的证据
自然发生的“人的行为”数据出现频率是有规律的,而加入人的主观意志干预后发生的数据,概率就特么变了,真是神知道一切啊。[呲牙]
Benford定律产生的原因是因为累加数据的十进位造成的,适用于所有1+1+1..这样一个个产生的数据。我可以解释一下:比方说密西根400个投票站,在投第一票的时候,所有的投票站都是1,这时候统计数据就是1的比例是100%。投第2票的时候,有的投票站产生了2,但是有的投票站产生了川普和拜登各是1,这时候1的占比也很大,2次之。如此下去,有些投票站投的快,会先到达10,这时候如果统计的票数,也是1最多。之后还会首先出现100、111,或者1111,总之累加的数据,1是先出现的,其次是2。按照Benford定律,1的占比概率是30%、2是17%,依次减少。
篡改数据的时候,作弊者不知道本福特定律,所以1和2用的太少了。看密西根的图,他们用了很多的5。
投票特别适合本福特定律,任意时段进行区间统计,都应该符合本福特定律。统计后清零然后继续统计,还是从1开始